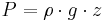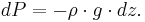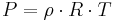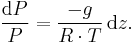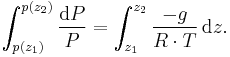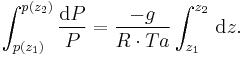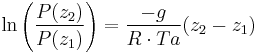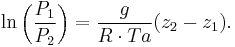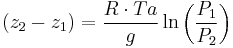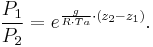Hypsometric equation

The hypsometric equation relates an atmospheric pressure ratio to the equivalent thickness of an atmospheric layer under the assumptions of constant temperature and gravity. It is derived from the hydrostatic equation and the ideal gas law.

It is expressed as:

$\ h = z_2 - z_1 = \frac{R \cdot T}{g} \cdot \ln \left [ \frac{P_1}{P_2} \right ]$

where:

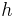$\ h$ = thickness of the layer [m]

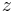$\ z$ = geopotential height [m]

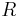$\ R$ = gas constant for dry air

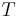$\ T$ = temperature in kelvins [K]

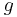$\ g$ = gravitational acceleration [m/s²]

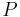$\ P$ = pressure [Pa]

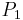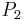In meteorology $P_1$ and $P_2$ are isobaric surfaces and T is the average temperature of the layer between them. In altimetry with the International Standard Atmosphere the hypsometric equation is used to compute pressure at a given geopotential height in isothermal layers in the upper and lower stratosphere.

Derivation

The hydrostatic equation:

$\ P = \rho \cdot g \cdot z$

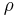where $\ \rho$ is the density [kg/m³], is used to generate the equation for hydrostatic equilibrium, written in differential form:

$dP = - \rho \cdot g \cdot dz.$

This is combined with the ideal gas law:

$\ P = \rho \cdot R \cdot T$

to eliminate 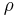$\ \rho$ :

$\frac{\mathrm{d}P}{P} = \frac{-g}{R \cdot T} \, \mathrm{d}z.$

This is integrated from 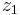$\ z_1$ to $\ z_2$ :

$\ \int_{p(z_1)}^{p(z_2)} \frac{\mathrm{d}P}{P} = \int_{z_1}^{z_2}\frac{-g}{R \cdot T} \, \mathrm{d}z.$

$\ \int_{p(z_1)}^{p(z_2)} \frac{\mathrm{d}P}{P} = \frac{-g}{R \cdot Ta}\int_{z_1}^{z_2} \, \mathrm{d}z.$

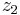Where Ta is equal to the average column temperature.

Integration gives:

$\ln \left( \frac{P(z_2)}{P(z_1)} \right) = \frac{-g}{R \cdot Ta} ( z_2 - z_1 )$

simplifying to:

$\ln \left( \frac{P_1}{P_2} \right) = \frac{g}{R \cdot Ta} ( z_2 - z_1 ).$

Rearranging:

$( z_2 - z_1 ) = \frac{R \cdot Ta}{g} \ln \left( \frac{P_1}{P_2} \right)$

or, eliminating the logarithm:

$\frac{P_1}{P_2} =e ^ { {g \over R \cdot Ta} \cdot ( z_2 - z_1 )}.$

References

AMS Glossary of Meteorology